4.21. Chapter 4 Spectroscopy#
4.22. Quantify Spectrum#
part of
MSE672: Introduction to Transmission Electron Microscopy
by Gerd Duscher, Spring 2023
Microscopy Facilities
Institute of Advanced Materials & Manufacturing
Materials Science & Engineering
The University of Tennessee, Knoxville
Background and methods to analysis and quantification of data acquired with transmission electron microscopes.
4.22.1. First we import the essential libraries#
All we need here should come with the annaconda or any other package
The xml library will enable us to read the Bruker file.
import sys
from pkg_resources import get_distribution, DistributionNotFound
def test_package(package_name):
"""Test if package exists and returns version or -1"""
try:
version = get_distribution(package_name).version
except (DistributionNotFound, ImportError) as err:
version = '-1'
return version
if test_package('pyTEMlib') < '0.2023.2.0':
print('installing pyTEMlib')
!{sys.executable} -m pip install --upgrade pyTEMlib -q
print('done')
done
%matplotlib ipympl
import matplotlib.pyplot as plt
import numpy as np
import xml.etree.ElementTree as ET
#
## import the configuration files of pyTEMlib (we need access to the data folder)
import pyTEMlib
import pyTEMlib.file_tools as ft
import pyTEMlib.eels_tools as eels
pyTEMlib.__version__
Symmetry functions of spglib enabled
'0.2023.2.0'
4.22.2. Cross-section for EDS in Transmission#
For thin samples such as used in transmission electron microscopy absorption, and fluorescence, can be neglected Chapter 2: Pennycook and Nellist, 2011. If multiple scattering and channelling is avoided the EDS partial scattering cross-section for a single atom of element x is given by Macarthur et al., 2015 and Macarthur et al., 2017:
Where:
\(N_x\): the volumetric number density of the elemental species being detected,
\(t\): the sample thickness (same length unit as volume in N_x),
\(I_x\): is the raw x-ray counts detected from the sample (a.u.),
\(i_0\): is the probe current (A),
\(\tau\) is the exposure time (s),
\(e\) is the electronic charge (C).
A more consistent way would be to relate the cross-section with areal density \(n_x\) and to use incident flux \(I_0\) like in the case of EELS earlier.
Where:
\(n_x = \rho_x *t \): the areal density of the elemental species being detected,
\(I_0 = i_0*\tau/e\): incident flux: total number of electrons the sample is exposed to during the experiment
4.22.2.1. Comparison with EELS#
Above formula is the same as derived for EELS earlier. The difference is that \(I_x^{EELS}\) is the number of electrons that scattered inelastically per energy transfer (and momentum transfer).
While \(I_x^{EDS}\) is the raw counts of X-rays that originate in the relaxation of excitation from a specific core level of element \(x\). This implies that the competing relaxation process of generation of Auger electrons is the same for all elements.
This is a fundamental requirement for quantification of both EDS and Auger spectroscopy.
The relationship between \(\sigma_{x}^{EDS}\) and \(\sigma_{x}^{EELS}\) is, therfore, a linear one. And we need to determine the efficiency of X-ray detection (not generation) per EDS system, which also has an take-off angle dependence.
However, the linear dependency is not between the EELS and EDS cross section as defined here, but the cross section of the core excitation, as introduced by Egerton. In that approach the inelastic scattering of lower-energy core-losses are approximated together with the background caused by plasmon losses.
Therefore, in the code cell below we need to subtract the background from lower-level excitations from the core-level in question.
z = 14
def get_eds_xsection(Xsection, energy_scale, start_bgd, end_bgd):
background = eels.power_law_background(Xsection, energy_scale, [start_bgd, end_bgd], verbose=False)
cross_section_core = Xsection- background[0]
cross_section_core[cross_section_core < 0] = 0.0
cross_section_core[energy_scale < end_bgd] = 0.0
return cross_section_core
energy_scale = np.arange(10,6000)
Xsection = eels.xsec_xrpa(energy_scale, 200, z, 10. )
edge_info = eels.get_x_sections(z)
if 'K1' in edge_info:
start_bgd = edge_info['K1']['onset']*.95
end_bgd = edge_info['K1']['onset']-5
K_eds_xsection = get_eds_xsection(Xsection, energy_scale, start_bgd, end_bgd)
if 'L3' in edge_info:
start_bgd = edge_info['L3']['onset']*.8
end_bgd = edge_info['L3']['onset']-5
L_eds_xsection = get_eds_xsection(Xsection, energy_scale, start_bgd, end_bgd)
if 'M5' in edge_info:
start_bgd = edge_info['L3']['onset']*.8
end_bgd = edge_info['L3']['onset']-5
M5_eds_xsection = get_eds_xsection(Xsection, energy_scale, start_bgd, end_bgd)
background = eels.power_law_background(Xsection, energy_scale, [80, 95], verbose=False)
plt.figure()
plt.plot(energy_scale, Si_Xsection , label='EELS X-section')
plt.plot(energy_scale, background[0], label='L-core background')
plt.plot(energy_scale, L_eds_xsection, label='L-level X-section')
plt.plot(energy_scale, K_eds_xsection, label='K-level X-section')
plt.xlim(20,3000)
plt.ylim(0, 2000)
plt.xlabel ('energy (eV)')
plt.ylabel('cross section (barns)')
plt.legend();
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In[8], line 28
26 background = eels.power_law_background(Xsection, energy_scale, [80, 95], verbose=False)
27 plt.figure()
---> 28 plt.plot(energy_scale, Si_Xsection , label='EELS X-section')
29 plt.plot(energy_scale, background[0], label='L-core background')
31 plt.plot(energy_scale, L_eds_xsection, label='L-level X-section')
File ~\Anaconda3\envs\mse672\lib\site-packages\matplotlib\pyplot.py:2748, in plot(scalex, scaley, data, *args, **kwargs)
2746 @_copy_docstring_and_deprecators(Axes.plot)
2747 def plot(*args, scalex=True, scaley=True, data=None, **kwargs):
-> 2748 return gca().plot(
2749 *args, scalex=scalex, scaley=scaley,
2750 **({"data": data} if data is not None else {}), **kwargs)
File ~\Anaconda3\envs\mse672\lib\site-packages\matplotlib\axes\_axes.py:1668, in Axes.plot(self, scalex, scaley, data, *args, **kwargs)
1425 """
1426 Plot y versus x as lines and/or markers.
1427
(...)
1665 (``'green'``) or hex strings (``'#008000'``).
1666 """
1667 kwargs = cbook.normalize_kwargs(kwargs, mlines.Line2D)
-> 1668 lines = [*self._get_lines(*args, data=data, **kwargs)]
1669 for line in lines:
1670 self.add_line(line)
File ~\Anaconda3\envs\mse672\lib\site-packages\matplotlib\axes\_base.py:311, in _process_plot_var_args.__call__(self, data, *args, **kwargs)
309 this += args[0],
310 args = args[1:]
--> 311 yield from self._plot_args(
312 this, kwargs, ambiguous_fmt_datakey=ambiguous_fmt_datakey)
File ~\Anaconda3\envs\mse672\lib\site-packages\matplotlib\axes\_base.py:504, in _process_plot_var_args._plot_args(self, tup, kwargs, return_kwargs, ambiguous_fmt_datakey)
501 self.axes.yaxis.update_units(y)
503 if x.shape[0] != y.shape[0]:
--> 504 raise ValueError(f"x and y must have same first dimension, but "
505 f"have shapes {x.shape} and {y.shape}")
506 if x.ndim > 2 or y.ndim > 2:
507 raise ValueError(f"x and y can be no greater than 2D, but have "
508 f"shapes {x.shape} and {y.shape}")
ValueError: x and y must have same first dimension, but have shapes (5990,) and (4990,)
4.22.2.2. Cross-section for EDS#
Of course we do not need the dependence of the cross section on energy but the sum.
The relevant functions will then be:
def get_eds_xsection(Xsection, energy_scale, start_bgd, end_bgd):
background = eels.power_law_background(Xsection, energy_scale, [start_bgd, end_bgd], verbose=False)
cross_section_core = Xsection- background[0]
cross_section_core[cross_section_core < 0] = 0.0
cross_section_core[energy_scale < end_bgd] = 0.0
return cross_section_core
def get_eds_cross_sections(z):
energy_scale = np.arange(10, 3700)
Si_Xsection = eels.xsec_xrpa(energy_scale, 200, z, 10.)
edge_info = eels.get_x_sections(z)
eds_cross_sections = {}
if 'K1' in edge_info:
start_bgd = edge_info['K1']['onset'] * 0.95
end_bgd = edge_info['K1']['onset'] - 5
K_eds_xsection = get_eds_xsection(Xsection, energy_scale, start_bgd, end_bgd)
eds_cross_sections['K'] = K_eds_xsection.sum() * 1e10
if 'L3' in edge_info:
start_bgd = edge_info['L3']['onset'] * 0.8
end_bgd = edge_info['L3']['onset'] - 5
L_eds_xsection = get_eds_xsection(Xsection, energy_scale, start_bgd, end_bgd)
eds_cross_sections['L'] = L_eds_xsection.sum() * 1e10
if 'M5' in edge_info:
start_bgd = edge_info['L3']['onset'] * 0.8
end_bgd = edge_info['L3']['onset'] - 5
M_eds_xsection = get_eds_xsection(Xsection, energy_scale, start_bgd, end_bgd)
eds_cross_sections['M'] = M_eds_xsection.sum() * 1e10
return eds_cross_sections
Si_eds_cross_sections = get_eds_cross_sections(14)
print('eds_cross_sections for Si core-levels:')
print(Si_eds_cross_sections)
print(f"ration of L to K cross sections {Si_eds_cross_sections['L']/Si_eds_cross_sections['K']:.1f}")
The above cross sections are for the excitation of a specific core-level of an atom. The sum of the experimental detected X-ray lines of one family are a fraction of those cross-sections.
Given the large discrepancy of excitation probabilities of the different core-levels, we use the lower-energy cross-sections if possible. Adding up the different families will result in sup-percent change in the total percentage of excitation probabilties.
Varambhia et al. used the linear thickness dependence of the signal to correlate the cross sections of EDS and EELS. This is an excellent way to callibrate the EDS system. And the correlation factor between EELS and EDS should be same for different X-Ray peak families of all elements. The similar method can be used to callibrate the cross section of ADF intensities.
4.22.2.3. Atomic-resolution EDS#
For atomic-resolution studies, an integration of the counts over a Voronoi cell in the EDX map gives a partial cross-section for that column, by analogy with the approach for ADF cross-sections (E et al., 2013). For comparison, the popularly used ΞΆ-factor method defined by (Watanabe et al., 2003) is:
Where
\(I_x\) is the raw x-ray counts,
Ο is the sample density in kg/m3,
t is the sample thickness,
\(C_x\) is the weight fraction of element x.
In Eq. (2), the definition of sample density in the zeta-factor approach is in kg/m3 which makes absolute quantification of nanoparticles, in terms of βnumber of atomsβ, cumbersome. Nonetheless, partial cross-section is very similar to the ΞΆ-factor and can be equated to it using Eq. (4). Where M is the molar mass (in kg/mol) and NA is Avogadroβs constant.
4.22.3. Open a EDS spectrum file#
Here the EDS.rto file in the example_data folder.
%matplotlib ipympl
import matplotlib.pyplot as plt
import numpy as np
fig, ax = plt.subplots()
x = np.linspace(0, 2*np.pi, 100)
y = np.sin(3*x)
ax.plot(x, y)
import ipympl
ipympl.__version__
'0.9.2'
from ipywidgets import IntSlider
IntSlider()
datasets = ft.open_file()
view = datasets['Channel_000'].plot()
plt.figure()
plt.plot([2,2],[1,3])
[<matplotlib.lines.Line2D at 0x1d06c71ec80>]
import ipympl
%gui qt
from PyQt5 import QtGui, QtWidgets
path = ''
fname, file_filter = QtWidgets.QFileDialog.getOpenFileName(None, "Select a file...", path)
import codecs
def open_Bruker(fname):
tree = ET.parse(fname)
root = tree.getroot()
spectrum_number = 0
i=0
image_count = 0
o_count = 0
tags = {}
for neighbor in root.iter():
#print(neighbor.attrib.keys())
if 'Type' in neighbor.attrib:
if 'verlay3' in neighbor.attrib['Type'] :
semImage = neighbor
#print(neighbor.attrib['Type'])
if 'Name' in neighbor.attrib:
print('\t',neighbor)
print('\t',neighbor.attrib['Type'])
print('\t',neighbor.attrib['Name'])
print('\t',neighbor.find("./ClassInstance[@Type='TRTSpectrumList']"))
#if 'TRTImageOverlay' in neighbor.attrib['Type'] :
if 'TRTCrossOverlayElement'in neighbor.attrib['Type'] :
if 'Spectrum' in neighbor.attrib['Name']:
#print(o_count)
o_count+=1
if 'overlay' not in tags:
tags['overlay']= {}
if 'image'+str(image_count) not in tags['overlay']:
tags['overlay']['image'+str(image_count)] ={}
tags['overlay']['image'+str(image_count)][neighbor.attrib['Name']] ={}
over = tags['overlay']['image'+str(image_count)][neighbor.attrib['Name']]
for child in neighbor.iter():
if 'verlay' in child.tag:
#print(child.tag)
pos = child.find('./Pos')
if pos != None:
over['posX'] = int(pos.find('./PosX').text)
over['posY'] = int(pos.find('./PosY').text)
#dd = neighbor.find('Top')
#print('dd',dd)
#print(neighbor.attrib)
if 'TRTImageData' in neighbor.attrib['Type'] :
#print('found image ', image_count)
dd = neighbor.find("./ClassInstance[@Type='TRTCrossOverlayElement']")
if dd != None:
print('found in image')
image = neighbor
if 'image' not in tags:
tags['image']={}
tags['image'][str(image_count)]={}
im = tags['image'][str(image_count)]
im['width'] = int(image.find('./Width').text) # in pixels
im['height'] = int(image.find('./Height').text) # in pixels
im['dtype'] = 'u' + image.find('./ItemSize').text # in bytes ('u1','u2','u4')
im['plane_count'] = int(image.find('./PlaneCount').text)
im['data'] = {}
for j in range( im['plane_count']):
#print(i)
img = image.find("./Plane" + str(i))
raw = codecs.decode((img.find('./Data').text).encode('ascii'),'base64')
array1 = np.frombuffer(raw, dtype= im['dtype'])
#print(array1.shape)
im['data'][str(j)]= np.reshape(array1,(im['height'], im['width']))
image_count +=1
if 'TRTDetectorHeader' == neighbor.attrib['Type'] :
detector = neighbor
tags['detector'] ={}
for child in detector:
if child.tag == "WindowLayers":
tags['detector']['window']={}
for child2 in child:
tags['detector']['window'][child2.tag]={}
tags['detector']['window'][child2.tag]['Z'] = child2.attrib["Atom"]
tags['detector']['window'][child2.tag]['thickness'] = float(child2.attrib["Thickness"])*1e-5 # stupid units
if 'RelativeArea' in child2.attrib:
tags['detector']['window'][child2.tag]['relative_area'] = float(child2.attrib["RelativeArea"])
#print(child2.tag,child2.attrib)
else:
#print(child.tag , child.text)
if child.tag != 'ResponseFunction':
if child.text !=None:
tags['detector'][child.tag]=child.text
if child.tag == 'SiDeadLayerThickness':
tags['detector'][child.tag]=float(child.text)*1e-6
#print(child.tag)
if child.tag == 'DetectorThickness':
tags['detector'][child.tag]=float(child.text)*1e-1
# ESMA could stand for Electron Scanning Microscope Analysis
if 'TRTESMAHeader' == neighbor.attrib['Type'] :
esma = neighbor
tags['esma'] ={}
for child in esma:
if child.tag in ['PrimaryEnergy', 'ElevationAngle', 'AzimutAngle', 'Magnification', 'WorkingDistance' ]:
tags['esma'][child.tag]=float(child.text)
if 'TRTSpectrum' == neighbor.attrib['Type'] :
if 'Name' in neighbor.attrib:
spectrum = neighbor
TRTHeader = spectrum.find('./TRTHeaderedClass')
if TRTHeader != None:
hardware_header = TRTHeader.find("./ClassInstance[@Type='TRTSpectrumHardwareHeader']")
spectrum_header = spectrum.find("./ClassInstance[@Type='TRTSpectrumHeader']")
#print(i, TRTHeader)
tags[spectrum_number] = {}
tags[spectrum_number]['hardware_header'] ={}
if hardware_header != None:
for child in hardware_header:
tags[spectrum_number]['hardware_header'][child.tag]=child.text
tags[spectrum_number]['detector_header'] ={}
tags[spectrum_number]['spectrum_header'] ={}
for child in spectrum_header:
tags[spectrum_number]['spectrum_header'][child.tag]=child.text
tags[spectrum_number]['data'] = np.fromstring(spectrum.find('./Channels').text,dtype='Q', sep=",")
spectrum_number+=1
return tags
tags = open_Bruker(fname)
spectrum1 =tags[0]['data']
spectrum2 =tags[1]['data']
offset = float(tags[0]['spectrum_header']['CalibAbs'])
scale = float(tags[0]['spectrum_header']['CalibLin'])
energy_scale1 = np.arange(len(spectrum1))*scale+offset
offset = float(tags[1]['spectrum_header']['CalibAbs'])
scale = float(tags[1]['spectrum_header']['CalibLin'])
energy_scale2 = np.arange(len(spectrum2))*scale+offset
plt.figure(figsize=(10,4))
ax1 = plt.subplot(1,2,1)
ax1.imshow(tags['image']['0']['data']['0'])
for key in tags['overlay']['image1']:
d = tags['overlay']['image1'][key]
ax1.scatter ([d['posX']], [d['posY']], marker="x", color='r')
ax1.text(d['posX']+5, d['posY']-5, key, color='r')
ax2 = plt.subplot(1,2,2)
plt.plot(energy_scale1,spectrum1, label = 'spectrum 1')
plt.plot(energy_scale2,spectrum2, label = 'spectrum 2')
plt.xlabel('energy [keV]')
plt.xlim(0,5)
plt.ylim(0)
plt.tight_layout()
plt.legend();
4.22.4. Peak Finding#
We can also use the peak finding routine of the scipy.signal to find all the maxima.
import scipy as sp
import scipy.signal as sig
start = np.searchsorted(energy_scale1, 0.125)
## we use half the width of the resolution for smearing
width = int(np.ceil(125*1e-3/2 /(energy_scale1[1]-energy_scale1[0])/2)*2+1)
new_spectrum = sp.signal.savgol_filter(spectrum1[start:], width, 2) ## we use half the width of the resolution for smearing
new_energy_scale = energy_scale1[start:]
major_peaks, _ = sp.signal.find_peaks(new_spectrum, prominence=1000)
minor_peaks, _ = sp.signal.find_peaks(new_spectrum, prominence=30)
peaks = major_peaks
spectrum1 = np.array(spectrum1)
plt.figure()
plt.plot(energy_scale1,spectrum1, label = 'spectrum 1')
#plt.plot(energy_scale1,gaussian_filter(spectrum1, sigma=1), label = 'filtered spectrum 1')
plt.plot(new_energy_scale,new_spectrum, label = 'filtered spectrum 1')
plt.scatter( new_energy_scale[minor_peaks], new_spectrum[minor_peaks], color = 'blue')
plt.scatter( new_energy_scale[major_peaks], new_spectrum[major_peaks], color = 'red')
plt.xlim(.126,5);
4.22.5. Peak identification#
Here we look up all the elemetns and see whether the position of major line (K-L3, K-L2β or βL3-M5β) coincides with a peak position as found above.
Then we plot all the lines of such an element with the appropriate weight.
The positions and the weight are tabulated in the ffast.pkl file introduced in the Characteristic X-Ray peaks notebook
import pickle
pkl_file = open('ffast.pkl', 'rb')
ffast = pickle.load(pkl_file)
pkl_file.close()
plt.figure()
#plt.plot(energy_scale1,spectrum2, label = 'spectrum 1')
#plt.plot(energy_scale1,gaussian_filter(spectrum1, sigma=1), label = 'filtered spectrum 1')
plt.plot(new_energy_scale,new_spectrum, label = 'filtered spectrum 1')
plt.xlim(0.1,4)
plt.ylim(-800)
plt.gca().axhline(y=0,color='gray', linewidth = 0.5);
out_tags = {}
out_tags['spectra'] = {}
out_tags['spectra'][0] = {}
out_tags['spectra'][0]['data'] = spectrum1
out_tags['spectra'][0]['energy_scale'] = energy_scale1
out_tags['spectra'][0]['energy_scale_start'] = start
out_tags['spectra'][0]['smooth_spectrum'] = new_spectrum
out_tags['spectra'][0]['smooth_energy_scale'] = new_energy_scale
out_tags['spectra'][0]['elements'] ={}
#print(ffast[6])
number_of_elements = 0
for peak in minor_peaks:
for element in range(1,93):
if 'K-L3' in ffast[element]['lines']:
if abs(ffast[element]['lines']['K-L3']['position']- new_energy_scale[peak]*1e3) <10:
out_tags['spectra'][0]['elements'][number_of_elements] = {}
out_tags['spectra'][0]['elements'][number_of_elements]['element'] = ffast[element]['element']
out_tags['spectra'][0]['elements'][number_of_elements]['found_lines'] = 'K-L3'
out_tags['spectra'][0]['elements'][number_of_elements]['lines'] = ffast[element]['lines']
out_tags['spectra'][0]['elements'][number_of_elements]['experimental_peak_index'] = peak
out_tags['spectra'][0]['elements'][number_of_elements]['experimental_peak_energy'] = new_energy_scale[peak]*1e3
number_of_elements += 1
plt.plot([ffast[element]['lines']['K-L3']['position']/1000.,ffast[element]['lines']['K-L3']['position']/1000.], [0,new_spectrum[peak]], color = 'red')
plt.text(new_energy_scale[peak],0, ffast[element]['element']+'\nK-L3', verticalalignment='top')
for line in ffast[element]['lines']:
if 'K' in line:
if abs(ffast[element]['lines'][line]['position']-ffast[element]['lines']['K-L3']['position'])> 20:
if ffast[element]['lines'][line]['weight']>0.07:
#print(element, ffast[element]['lines'][line],new_spectrum[peak]*ffast[element]['lines'][line]['weight'])
plt.plot([ffast[element]['lines'][line]['position']/1000.,ffast[element]['lines'][line]['position']/1000.], [0,new_spectrum[peak]*ffast[element]['lines'][line]['weight']], color = 'red')
plt.text(ffast[element]['lines'][line]['position']/1000.,0, ffast[element]['element']+'\n'+line, verticalalignment='top')
elif 'K-L2' in ffast[element]['lines']:
if abs(ffast[element]['lines']['K-L2']['position']- new_energy_scale[peak]*1e3) <10:
plt.plot([new_energy_scale[peak],new_energy_scale[peak]], [0,new_spectrum[peak]], color = 'orange')
plt.text(new_energy_scale[peak],0, ffast[element]['element']+'\nK-L2', verticalalignment='top')
out_tags['spectra'][0]['elements'][number_of_elements] = {}
out_tags['spectra'][0]['elements'][number_of_elements]['element'] = ffast[element]['element']
out_tags['spectra'][0]['elements'][number_of_elements]['found_lines'] = 'K-L2'
out_tags['spectra'][0]['elements'][number_of_elements]['lines'] = ffast[element]['lines']
out_tags['spectra'][0]['elements'][number_of_elements]['experimental_peak_index'] = peak
out_tags['spectra'][0]['elements'][number_of_elements]['experimental_peak_energy'] = new_energy_scale[peak]*1e3
number_of_elements += 1
if 'L3-M5' in ffast[element]['lines']:
if abs(ffast[element]['lines']['L3-M5']['position']- new_energy_scale[peak]*1e3) <10:
pass
print('found_element', element,ffast[element]['lines']['L3-M5']['position'], new_energy_scale[peak] )
#plt.scatter( new_energy_scale[peak], new_spectrum[peak], color = 'blue')
out_tags['spectra'][0]['elements'][number_of_elements] = {}
out_tags['spectra'][0]['elements'][number_of_elements]['element'] = ffast[element]['element']
out_tags['spectra'][0]['elements'][number_of_elements]['found_lines'] = 'L3-M5'
out_tags['spectra'][0]['elements'][number_of_elements]['lines'] = ffast[element]['lines']
out_tags['spectra'][0]['elements'][number_of_elements]['experimental_peak_index'] = peak
out_tags['spectra'][0]['elements'][number_of_elements]['experimental_peak_energy'] = new_energy_scale[peak]*1e3
number_of_elements += 1
for element in out_tags['spectra'][0]['elements']:
print(out_tags['spectra'][0]['elements'][element]['element'],out_tags['spectra'][0]['elements'][element]['found_lines'])
found_element 51 3604.7 3.597909755
C K-L2
O K-L3
Mg K-L3
Al K-L3
P K-L3
S K-L3
K K-L3
Sb L3-M5
Using that we get for all peaks in the low energy region:
from scipy.interpolate import interp1d
import scipy.constants as const
tags={'detector': { 'window': {'0': {'Z': 6,
'thickness': 100}
},
'SiDeadLayerThickness': 20
}
}
def detector_efficiency(tags, energy_scale):
detector_Efficiency1 = np.ones(len(energy_scale))
for key in tags['detector']['window']:
Z = int(tags['detector']['window'][key]['Z'])
if Z < 14:
t = tags['detector']['window'][key]['thickness']
## interpolate mass absorption coefficient to our energy scale
lin = interp1d(ffast[Z]['E']/1000.,ffast[Z]['photoabsorption'],kind='linear')
mu = lin(energy_scale) * ffast[Z]['nominal_density']*100. #1/cm -> 1/m
detector_Efficiency1 = detector_Efficiency1 * np.exp(-mu * t)
print(Z,t)
t = float(tags['detector']['SiDeadLayerThickness'])*1e-6
print(t)
t = .30*1e-7
print(t)
lin = interp1d(ffast[14]['E']/1000.,ffast[14]['photoabsorption'],kind='linear')
mu = lin(energy_scale) * ffast[14]['nominal_density']*100. #1/cm -> 1/m
detector_Efficiency1 = detector_Efficiency1 * np.exp(-mu * t)
detector_thickness = float(tags['detector']['DetectorThickness'])*1e-1
## interpolate mass absorption coefficient to our energy scale
mu_Si = lin(energy_scale) * ffast[14]['nominal_density']*100. #1/cm -> 1/m
print(detector_thickness)
detector_Efficiency2 = (1.0 - np.exp(-mu * detector_thickness))# * oo4pi;
return detector_Efficiency1*detector_Efficiency2
detector_Efficiency = detector_efficiency(tags, new_energy_scale)
plt.figure()
plt.plot(new_energy_scale*1000, detector_Efficiency)
plt.xlim(0,2000)
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[1], line 42
38 detector_Efficiency2 = (1.0 - np.exp(-mu * detector_thickness))# * oo4pi;
41 return detector_Efficiency1*detector_Efficiency2
---> 42 detector_Efficiency = detector_efficiency(tags, new_energy_scale)
44 plt.figure()
45 plt.plot(new_energy_scale*1000, detector_Efficiency)
NameError: name 'new_energy_scale' is not defined
Peaks = []
elements_peaks = []
intensities = []
for element in out_tags['spectra'][0]['elements']:
el_dict = out_tags['spectra'][0]['elements'][element]
position = el_dict['lines'][el_dict['found_lines']]['position']
weight = 0
for line in el_dict['lines']:
if abs(position - el_dict['lines'][line]['position'])<20:
weight += el_dict['lines'][line]['weight']
index = np.searchsorted(new_energy_scale,el_dict['lines'][el_dict['found_lines']]['position']/1000.)
intensity = new_spectrum[index]/weight
added_peaks = np.zeros(len(new_energy_scale))
for line in el_dict['lines']:
if line[0] == el_dict['found_lines'][0]:
if el_dict['lines'][line]['weight']> 0.01:
p = getPeak(el_dict['lines'][line]['position']/1000.,new_energy_scale)*el_dict['lines'][line]['weight']
Peaks.append(p)
added_peaks = added_peaks + p
elements_peaks.append(added_peaks)
intensities.append(intensity)
plt.figure()
plt.plot(new_energy_scale,new_spectrum, label = 'filtered spectrum 1',color='red')
for i in range(len(elements_peaks)):
plt.plot(new_energy_scale,elements_peaks[i]*intensities[i], label = f'Peak{i}')
pass
peaks = np.array(Peaks)
plt.plot(new_energy_scale,peaks.sum(axis=0), label = f'Peaks', color = 'blue')
print(peaks.shape)
#plt.xlim(0,5)
offset = float(tags[0]['spectrum_header']['CalibAbs'])
scale = float(tags[0]['spectrum_header']['CalibLin'])
energy_scale1 = np.arange(len(spectrum1))*scale+offset
p = [1, 37, .3, offset, scale]
E_0= 20
E = new_energy_scale
N = detector_Efficiency * (p[0] + p[1]*(E_0-E)/E + p[2]*(E_0-E)**2/E)
N = de * (p[0] + p[1]*(E_0-E)/E + p[2]*(E_0-E)**2/E)
pp = p[0:5].copy()
for i in range(len(elements_peaks)):
pp.append(intensities[i])
plt.plot(new_energy_scale,N, color= 'orange')
plt.xlim(0,4)
detector_Efficiency = de
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[2], line 4
2 elements_peaks = []
3 intensities = []
----> 4 for element in out_tags['spectra'][0]['elements']:
5 el_dict = out_tags['spectra'][0]['elements'][element]
7 position = el_dict['lines'][el_dict['found_lines']]['position']
NameError: name 'out_tags' is not defined
def model(p,energy_scale):
E = energy_scale
spectrum = detector_Efficiency * (p[0] + p[1]*(E_0-E)/E + p[2]*(E_0-E)**2/E)
for i in range(5,len(p)):
spectrum = spectrum+elements_peaks[i-5]*abs(p[i])
return spectrum
def getFWHM(E):
return np.sqrt(2.5*(E-E_ref)+FWHM_ref**2)
def gaussian(enrgy_scale, mu, FWHM):
sig = FWHM/2/np.sqrt(2*np.log(2))
return np.exp(-np.power(enrgy_scale - mu, 2.) / (2 * np.power(sig, 2.)))
def getPeak(E, energy_scale):
E_ref = 5895.0
FWHM_ref = 136 #eV
FWHM = np.sqrt(2.5*(E*1e3-E_ref)+FWHM_ref**2)*1e-3
return gaussian(energy_scale, E, FWHM)
Peaks = []
elements_peaks = []
intensities = []
for element in out_tags['spectra'][0]['elements']:
el_dict = out_tags['spectra'][0]['elements'][element]
position = el_dict['lines'][el_dict['found_lines']]['position']
weight = 0
for line in el_dict['lines']:
if abs(position - el_dict['lines'][line]['position'])<20:
weight += el_dict['lines'][line]['weight']
index = np.searchsorted(new_energy_scale,el_dict['lines'][el_dict['found_lines']]['position']/1000.)
intensity = new_spectrum[index]/weight
added_peaks = np.zeros(len(new_energy_scale))
for line in el_dict['lines']:
if line[0] == el_dict['found_lines'][0]:
if el_dict['lines'][line]['weight']> 0.01:
p = getPeak(el_dict['lines'][line]['position']/1000.,new_energy_scale)*el_dict['lines'][line]['weight']
Peaks.append(p)
added_peaks = added_peaks + p
elements_peaks.append(added_peaks)
intensities.append(intensity)
p = [1, 37, .3, offset, scale]
E_0= 20
E = new_energy_scale
N = detector_Efficiency * (p[0] + p[1]*(E_0-E)/E + p[2]*(E_0-E)**2/E)
pp = p[0:5].copy()
for i in range(len(elements_peaks)):
pp.append(intensities[i])
spectrum3 = model(pp[:-1],new_energy_scale)
plt.figure()
plt.plot(new_energy_scale,new_spectrum, label = 'filtered spectrum 1',color='red')
plt.plot(new_energy_scale, spectrum3)
plt.xlim(0,4)
(0.0, 4.0)
from scipy.optimize import leastsq
## background fitting
def specfit(p, y, x):
err = y - model(p,x)
return err
p, lsq = leastsq(specfit, pp[:-1], args=(new_spectrum, new_energy_scale), maxfev=2000)
print( f'element\t end \t start ')
for i, element in enumerate(out_tags['spectra'][0]['elements']):
if i<len(p)-5:
el_dict = out_tags['spectra'][0]['elements'][element]
print(f"{el_dict['element']:2s}: \t {abs(p[i+5]):6.2f} \t {pp[i+5]:.2f}")
#print(p,pp)
element end start
C : 16487.64 16444.49
O : 3267.00 3274.63
Mg: 2831.85 3127.80
Al: 84.40 334.63
P : 5267.50 5499.66
S : 82.35 234.96
K : 2526.57 2693.25
spectrum3 = model(p,new_energy_scale)
plt.figure()
plt.plot(new_energy_scale,new_spectrum, label = 'filtered spectrum 1',color='red')
plt.plot(new_energy_scale, spectrum3)
plt.plot(new_energy_scale, new_spectrum-spectrum3)
plt.gca().axhline(y=0,color='gray');
plt.xlim(0,4);
4.22.6. Energy Scale#
What happened?
4.23. Composition Basis#
4.23.1. Castaingβs first approximation:#
\(πΆ_i\) = Concentration of element \(π\)
\(πΌ_π\) = X-ray intensity of element \(π\) in the sample
\(πΌ_{ππ’ππ}\) = X-ray intensity of a pure sample of the element
We call the ratio: \(\frac{I_i}{I_{Pure}}\) k-ratio
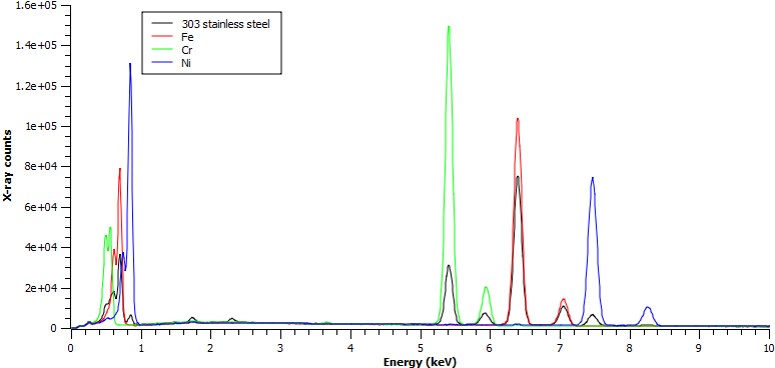
Stainless to Fe-Ka ratio = 0.745
Stainless to Cr-Ka ratio = 0.208
Stainless to Ni-Ka ratio = 0.080
therefore:
Fe: 70.8 wt%
Cr: 17.2 wt%
Ni: 9.1 wt%
4.24. ZAF Correction#
While the k-ratio is a good starting point, the basic approximation does not take absorption and interaction between the different elements into account. To increase the precision the following corrections are applied:
Z: Atomic number factor
A: sample Absorption
F: Fluorescence
4.24.1. Atomic Number Factor - Z#
The stopping power is equal to the energy loss of the electron per unit length it travels in the material: \(π(πΈ)=βππΈ/πt\)
D.C. Joy, Microsc. Microanal. 7(2001): 159-169
\(E\): electron energy
\(\rho\): density of material
\(Z\): Atomic number
\(A\): atomic weight of material
\(J\): Mean ionizaton potential
The backscatter correction is the relation between how many photons are generated with and without backscattering.
\(R\): backscatter correction
\(Z\): Mean atomic number of sample
\(E_0\): electron energy
\(E_c\): critical ionization energy
4.24.2. Absorption Correction#
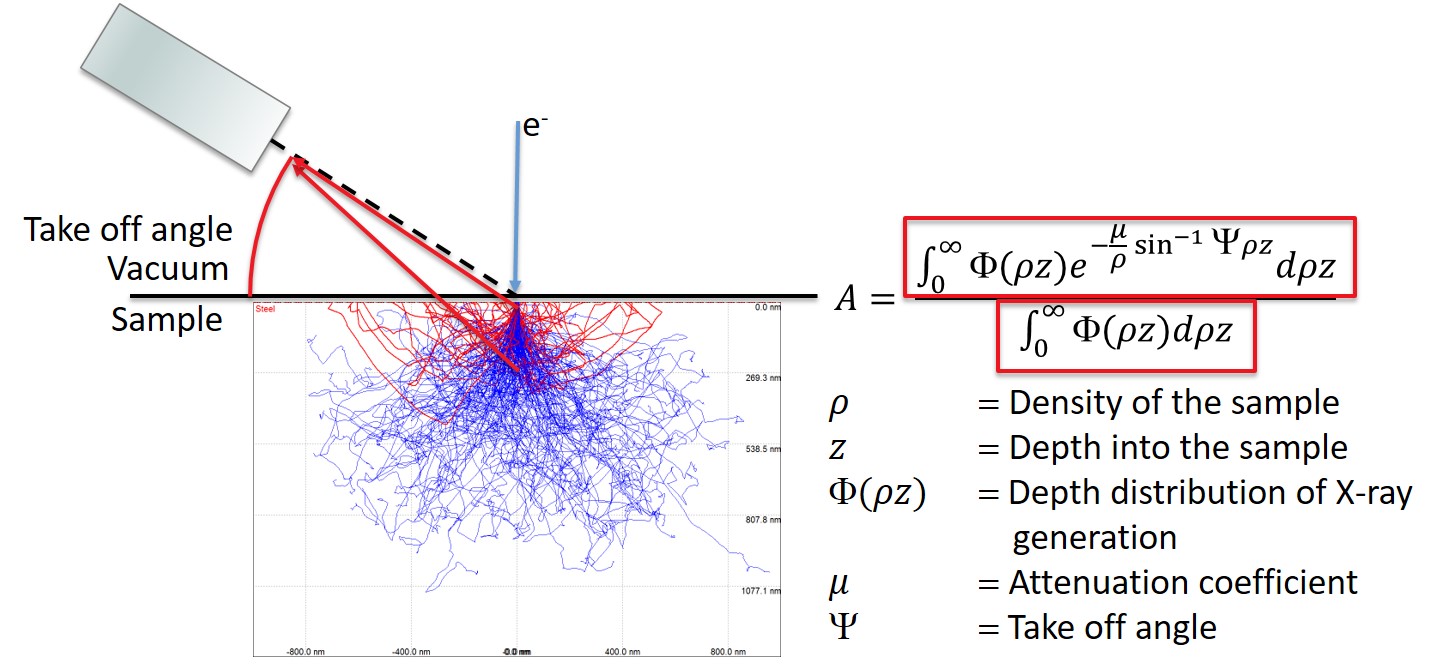
The numerator describes how many X-rays are generated at a given depth and scales the number by the attenuation due to the escape path in the sample.
The denominator is the total number of X-rays generated without attenuation.
This means that A is a normalized value that describes how many of the generated X-rays actually escaped the sample.
4.24.3. Fluorescence Correction#
The high energy X-ray can originate from characteristic X-rays from elements with higher energy lines or from the bremsstrahlung. This means that even the element with the highest energy line can have a fluorescence correction.
4.24.4. Using ZAF#
4.24.5. ZAF assumptions#
Several assumptions are made either directly or indirectly in the equations used to calculate the composition of a sample.
The sample is homogenous.
The density π and the mass attenuation π/π is assumed to be constant.
The sample is flat.
π§ is well defined for any given position and no additional absorption takes place after the X-ray reaches the sample surface.
The sample is infinitely thick as seen by the electron beam.
-The energy of the incident electron is deposited in the sample and only secondary and backscatter electrons escape.
4.25. Composition Standardless#
For standard-less analysis the k-ratio is either calculated in the software or based on internal standards.
Following
to calculate the mass concentration \(C_i\) from the intensity of a line (\(I_{ch}\)), we use:
\(\omega\) : fluorescence yield
\(N_A\): Avogadroβs number
\(\rho\): density
\(C_i\): mass concentration of element \(i\)
\(A\):atomic weight
\(R\): backscatter loss
\(Q_i\): ionization cross section
\(dE/ds\): rate of energy loss
\(E_0\): incident beam energy
\(E_c\): excitation energy
\(\epsilon\): EDS efficiency
where: \(N_A * \rho * C_i/A\): volume density of element \(i\) (atoms per unit volume)
What do we know at this point?
\(\omega; N_A; \rho; A; Q_i; E_0; E_c;\) and \(\epsilon\)
def BrowningEmpiricalCrossSection(elm , energy):
""" * Computes the elastic scattering cross section for electrons of energy between
* 0.1 and 30 keV for the specified element target. The algorithm comes from<br>
* Browning R, Li TZ, Chui B, Ye J, Pease FW, Czyzewski Z & Joy D; J Appl
* Phys 76 (4) 15-Aug-1994 2016-2022
* The implementation is designed to be similar to the implementation found in
* MONSEL.
* Copyright: Pursuant to title 17 Section 105 of the United States Code this
* software is not subject to copyright protection and is in the public domain
* Company: National Institute of Standards and Technology
* @author Nicholas W. M. Ritchie
* @version 1.0
*/
Modified by Gerd Duscher, UTK
"""
#/**
#* totalCrossSection - Computes the total cross section for an electron of
#* the specified energy.
#*
# @param energy double - In keV
# @return double - in square meters
#*/
e = energy #in keV
re = np.sqrt(e);
return (3.0e-22 * elm**1.7) / (e + (0.005 * elm**1.7 * re) + ((0.0007 * elm**2) / re));
4.25.1. Summary#
EDS quantification is not magic and the results will highly depend on sample preparation and correct peak identification.
Correct quantification with ZAF relies on the sample being:
Flat
Homogenous
Infinitely thick to the electron beam
Use of standards is not required for good quantification but it will give additional information and increase quality of the results.
Peak-to-background based ZAF is good for rough samples but requires better spectra than regular ZAF.
The best way to good EDS results:
Good samples
Thorough sample preparation
Exact SEM Parameters