Chapter 4 Spectroscopy

4.12. Chapter 4 Spectroscopy #

4.13. Generation of Characteristic X-Rays#

part of

MSE672: Introduction to Transmission Electron Microscopy

Spring 2024

Gerd Duscher	Khalid Hattar
Microscopy Facilities	Tennessee Ion Beam Materials Laboratory
Materials Science & Engineering	Nuclear Engineering
Institute of Advanced Materials & Manufacturing
The University of Tennessee, Knoxville

Background and methods to analysis and quantification of data acquired with transmission electron microscopes.

4.13.1. Load relevant python packages#

4.13.1.1. Check Installed Packages#

import sys
import importlib.metadata
def test_package(package_name):
    """Test if package exists and returns version or -1"""
    try:
        version = importlib.metadata.version(package_name)
    except importlib.metadata.PackageNotFoundError:
        version = '-1'
    return version

if test_package('pyTEMlib') < '0.2024.2.3':
    print('installing pyTEMlib')
    !{sys.executable} -m pip install  --upgrade pyTEMlib -q

print('done')

done

4.13.2. First we import the essential libraries#

All we need here should come with the annaconda or any other package

%matplotlib widget
import matplotlib.pyplot as plt
import numpy as np
import sys
import os
if 'google.colab' in sys.modules:
    from google.colab import output
    from google.colab import drive
    output.enable_custom_widget_manager()
    
from pyTEMlib.xrpa_x_sections import x_sections

__notebook__ = 'CH4_14-Characteristic-X_Rays'
__notebook_version__ = '2019_08_21'

4.13.3. X-Ray Families#

The case is not always as simple as in the case of the carbon atom in the Introduction

As the atomic number $Z$ increases the number of electrons in the respective energy states increases. With increasing complexity of the shell structure more options for relaxtions are available with different probabilities.

For example a Na atom which has an M-shell The 1s state can be filled by an L- or an M-shell, producing two different characteristic X-rays:

K-L $_{2, 3} ($ K\alpha $) :$ E_X = $E_{K} - E_{L}$ = 104 eV
K-M $_{2, 3} ($ K\beta $) :$ E_X = $E_{K} - E_{M}$ = 1071 eV

For heavier atoms than sodium more options exist:

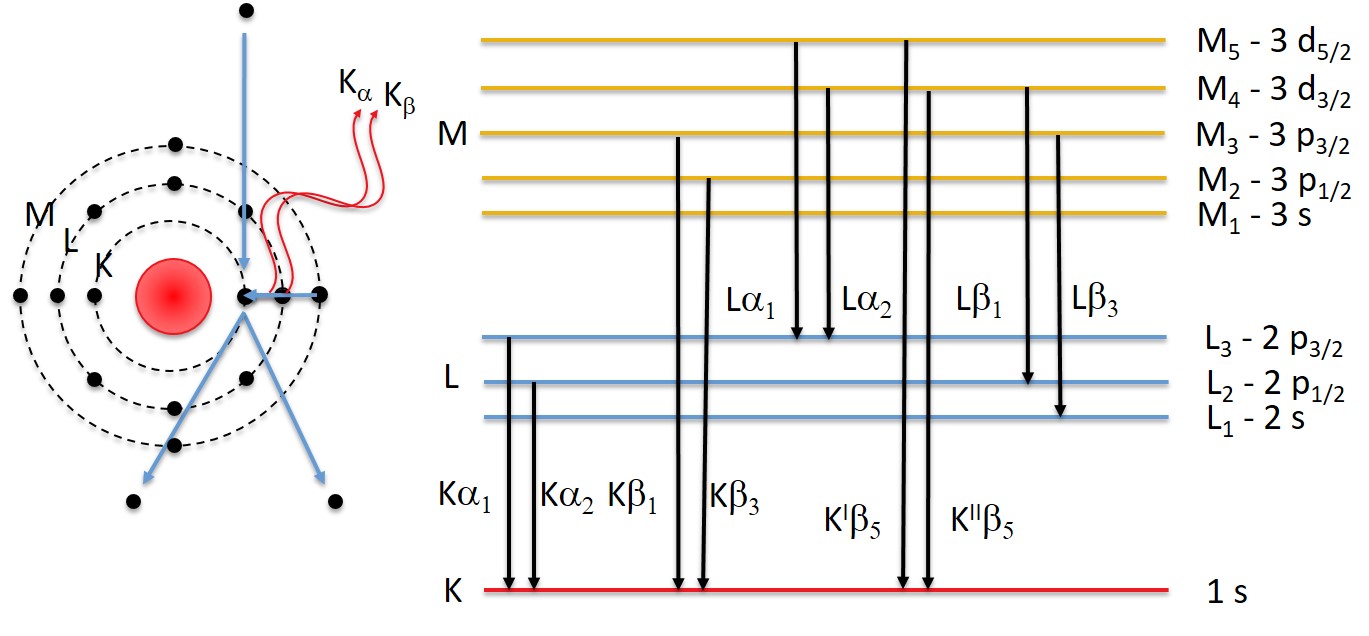
Nomenclature

4.13.4. X-ray Nomenclature#

Two systems are in use for naming characteristic X-ray lines.

The oldest one is the Siegbahn system in wich first the shell where the ionization occured is listed and then a greek letter that suggests the order of their families by their relative intensity ( $α > β > γ > η > ζ$ ).

For closely related memebers of a family additionally numebrs are attched such as $L β_{1}$ .

While most commercial software still uses the Siegbahn system the International Union of Pure and Applied Chemistry (IUPAC) has officially changed the system to a protocol that first dentoes the subshell were the ionization occured and followed with the term that indicates from which subshell the relaxation originates.

So $K α_{1}$ is replaced by $K - L_{3}$ .

eds-lines

Siegbahn	—–IUPAC—–	Siegbahn	—–IUPAC—–	Siegbahn	—–IUPAC—–
$K α_{1}$	$K - L_{3}$	$L α_{1}$	$L_{3} - M_{5}$	$M α_{1}$	$M_{5} - N_{7}$
$K α_{2}$	$K - L_{2}$	$L α_{2}$	$L_{3} - M_{4}$	$M α_{2}$	$M_{5} - N_{6}$
$K β_{1}$	$K - M_{3}$	$L β_{1}$	$L_{2} - M_{4}$	$M β$	$M_{4} - N_{6}$
$K β_{2}$	$K - N_{2, 3}$	$L β_{2}$	$L_{3} - N_{5}$	$M γ$	$M_{3} - N_{5}$
		$L β_{3}$	$L_{1} - M_{3}$	$M ζ$	$M_{4, 5} - N_{2, 3}$
		$L β_{4}$	$L_{1} - M_{2}$		$M_{3} - N_{1}$
		$L γ_{1}$	$L_{2} - N_{4}$		$M_{2} - N_{1}$
		$L γ_{2}$	$L_{1} - N_{2}$		$M_{3} - N_{4, 5}$
		$L γ_{3}$	$L_{1} - N_{3}$		$M_{3} - O_{1}$
		$L γ_{4}$	$L_{1} - O_{4}$		$M_{3} - O_{4, 5}$
		$L ζ$	$L_{2} - M_{1}$		$M_{2} - N_{4}$
		$L ι$	$L_{3} - M_{1}$

4.13.5. X-ray Weight of Lines#

Within the excitation probaility of the characteristic X-ray lines are not equal.

For sodium (see above for energies), the ratio of $K - L_{2, 3}$ to $K - M$ is approximatively 150: 1.

This ratios between the lines are a strong function of the atomic number $Z$ .

We load the data of the X-Ray lines from data from NIST, the line weights are taken from the Program DTSA-II, which is the quasi-standard in EDS analysis.

K_M5 = []
ele_K_M5 = []
L3_M1 = []
ele_M3_M1 = []
L1_N3 = []
ele_L1_N3 = []
L3_N5 =[]
ele_L3_N5 = []
L2_M4 = []
ele_L2_M4 = []
for element in range(5,82):
    if 'K-M5' in x_sections[str(element)]['lines']:
        K_M5.append(x_sections[str(element)]['lines']['K-M5']['weight']/x_sections[str(element)]['lines']['K-L3']['weight'])
        ele_K_M5.append(element)
    if 'L3-M5' in x_sections[str(element)]['lines']:
    
        if 'L3-M1' in x_sections[str(element)]['lines']:
            L3_M1.append(x_sections[str(element)]['lines']['L3-M1']['weight']/x_sections[str(element)]['lines']['L3-M5']['weight'])
            ele_M3_M1.append(element)
        
        if 'L1-N3' in x_sections[str(element)]['lines']:
            L1_N3.append(x_sections[str(element)]['lines']['L1-N3']['weight']/x_sections[str(element)]['lines']['L3-M5']['weight'])
            ele_L1_N3.append(element)
        
        if 'L3-N5' in x_sections[str(element)]['lines']:
            L3_N5.append(x_sections[str(element)]['lines']['L3-N5']['weight']/x_sections[str(element)]['lines']['L3-M5']['weight'])
            ele_L3_N5.append(element)
        
        if 'L2-M4' in x_sections[str(element)]['lines']:
            L2_M4.append(x_sections[str(element)]['lines']['L2-M4']['weight']/x_sections[str(element)]['lines']['L3-M5']['weight'])
            ele_L2_M4.append(element)
    
ele = np.linspace(1,94,94)

plt.figure()
plt.plot(ele_K_M5 ,K_M5, label = 'K-M$_3$ / K-L$_3$')
plt.plot(ele_M3_M1,L3_M1, label = 'L$_3$-M$_1$ / L$_3$-M$_5$')
plt.plot(ele_L1_N3,L1_N3, label = 'L$_1$-N$_3$ / L$_3$-M$_5$')
plt.plot(ele_L3_N5,L3_N5, label = 'L$_3$-N$_5$ / L$_3$-M$_5$')
plt.plot(ele_L2_M4,L2_M4, label = 'L$_2$-M$_4$ / L$_3$-M$_5$')
plt.ylabel('')
plt.gca().set_yscale('log')
plt.xlabel('atomic number')
plt.ylabel('relative weights of lines')

plt.legend();

4.13.6. Characteristic X-ray Intensity#

The cross section $Q_{I}$ (probability of excitation expressed as area) of an isolated atom ejecting an electron bound with energy $E_{c}$ (keV) by an electron with energy $E$ (keV) is:

Q_{I} (\frac{i o n i z a t i o n s}{e^{-} (a t o m s / c m^{2})}) = 6.51 \times 10^{- 20} [\frac{n_{s} b_{s}}{E E_{c}}] \log_{e} (c_{s} E / E_{c})

where:

$n_{s}$ : number of electrons in shell or subshell $s$
$b_{s}$ , $c_{s}$ : constants for a given shell $s$
$E$ : energy of the exciting electron
$E_{𝑐}$ : Critical ionization energy

For example for a K shell (Powell 1979): $n_{K} = 2$ , $b_{K} = 0.35$ , and $c_{k} = 1$

For silion the characteristic energy or binding energy for the K shell: $E_{c} = 1.838$ keV

The relationship between energy of the exciting electron and critical energy is important and is expressed as overvoltage $U$ : $ $U = \frac{E}{E_{c}}$ $

The overvoltage of the primary electron with energy $E_{0}$ is expressed as: $ $U_{0} = \frac{E_{0}}{E_{c}}$ $

We can express the cross section with the overvoltage:

Q_{I} = 6.51 \times 10^{- 20} [\frac{n_{s} b_{s}}{U E_{c}^{2}}] \log_{e} (c_{s} U)

n_K = 2.0
b_K = 0.35
c_K = 1.0

# Silicon
E_c_Si = 1.838 
# Iron
E_c_Fe = 6.401

E = np.linspace(0,30,2048)+0.05
U = E/E_c_Si

Q_Si = 6.51*1e-20*n_K*b_K/(U * E_c_Si**2)* np.log(c_K * U)
U = E/E_c_Fe
Q_Fe = 6.51*1e-20*n_K*b_K/(U * E_c_Fe**2)* np.log(c_K * U)
plt.figure()
plt.plot(E,Q_Si, label ='Si')
plt.plot(E,Q_Fe, label ='Fe')

plt.ylim(0.,Q_Si.max()*1.1)
plt.xlabel('excitation energy (keV)')
plt.ylabel('Q (inizations/[e$^-$ (atoms /cm$^2$)])')
plt.legend();

C.J. Powell,”Cross sections for inelastic electron scattering in solids”, Ultramicroscopy 28 pp 24-31 (1989)

E. Casnati, A. Tartari, and C. Baraldi; J. Phys. B: At. Mol. Phys..li (1982) 155-167: An empirical approach to K-shell ionisation cross section by electrons

D. Bote and F. Salvat “Calculations of inner-shell ionization by electron impact with the distorted-wave and plane-wave Born approximations”,Phys. Rev. A 77, 042701

x_sections['25']['M4']

{'filename': 'None',
 'excl before': 5,
 'excl after': 50,
 'onset': 7.26159,
 'factor': 0.6666666666666666}

 """        
 (Casnati's equation) was found to fit cross-section data to
 typically better than +-10% over the range 1<=Uk<=20 and 6<=Z<=79."
 
 Note: This result is for K shell. L & M are much less well characterized.
 C. Powell indicated in conversation that he believed that Casnati's
 expression was the best available for L & M also.
"""
shell_occupancy={'K':2,'L1':2,'L2':2,'L3':4,'M1':2,'M1':2,'M2':2,'M3':4,'M4':4,'M5':6}
import scipy.constants as const
res = 0.0;
beamE = 30
rel = []
Z= []
shell = 'M4'
for element in range(25,56):
    ee = x_sections[str(element)][shell]['onset']#getEdgeEnergy();
    u =  ee/beamE;
    #print(u)
    if(u > 1.0):
        u2 = u * u;
        phi = 10.57 * np.exp((-1.736 / u) + (0.317 / u2));
        #psi = Math.pow(ee / PhysicalConstants.RydbergEnergy, -0.0318 + (0.3160 / u) + (-0.1135 / u2));
        psi = np.power(ee / const.Rydberg, -0.0318 + (0.3160 / u) + (-0.1135 / u2));

        i = ee / const.electron_mass# PhysicalConstants.ElectronRestMass;
        t = beamE / const.electron_mass#PhysicalConstants.ElectronRestMass;
        f = ((2.0 + i) / (2.0 + t)) * np.sqrt((1.0 + t) / (1.0 + i)) * np.power(((i + t) * (2.0 + t) * np.sqrt(1.0 + i))/ ((t * (2.0 + t) * np.sqrt(1.0 + i)) + (i * (2.0 + i))), 1.5);
        getGroundStateOccupancy = shell_occupancy[shell]
        res = ((getGroundStateOccupancy * np.sqrt((const.value('Bohr radius') * const.Rydberg) / ee) * f * psi * phi * np.log(u)) / u);
        
        rel.append(res)
        Z.append(element)
    #print(res)
    
plt.figure()
plt.title(f"Casnati's cross section for beam energy {beamE:.0f} keV")
plt.plot(Z,rel)

plt.xlabel('atomic number Z')
plt.ylabel('Q [barns]');

Even though the cross section raises fast with overvoltage $U$ , too low overvoltage leads to a small cross section, which results in poor excitation of the X-ray line.

We can also see that the intial overvoltage $U_{0}$ varies with atomic number $Z$ , which will affect the relative generation of X-rays from different elements.

4.13.7. X-ray Production in a Thick Solid Sample#

If the sample is sufficient thick so that all electrons interact ( several micrometers) the X-ray intensity is found to follow an expression fo the form:

I \approx i_{p} {[(E_{0} - E_{c}) / E_{0}]}^{n} \approx i_{p} [U_{0} - 1]^{n}

where:

$i_{p}$ : beam current
$n$ : exponent $n$ depends on particular element and shell (Lifshin et al. 1980)

The exponent $n$ is ususally between 1.5 and 2. See what changes in the plot below if you change this exponent.

n = 1.5

U_0 = np.linspace(1,10, 2048)
i_p = 1.0 # in nA
I = i_p * (U_0-1.0)**n

plt.figure()
plt.plot(U_0,I)
plt.axhline(y=0., color='gray', linewidth=0.5)
plt.xlabel('overvoltage $U_0$ [kV]')
plt.ylabel('$I$ [nA]');

4.13.8. X-ray Production in a Thin Foil#

Now we have all the ingeedients to look at the total generation of X-rays.

The number of photons $n_{X}$ produced in a thin foil of thickness $t$ is : $ $n_{x} = Q_{I} (E) ω N_{A} \frac{1}{A} ρ t$ $

$n_{X}$ [photons/e $^{-}$ ]
$Q_{I} (E)$ [ ionizations/e $^{-}$ (atoms / cm $^{2}$ )): ionization cross section
$ω$ [X-rays/ ionization]: fluorescent yield = number of X-rays generated per ionization
$N_{A}$ [atoms per mol]: Avogadro’s number
$A$ [g/moles]: atomic weight
$ρ$ [g/cm $^{3}$ ]: density of sample
$t$ [cm]: thickness of sample

The number of X-rays increase linearly with the number of atoms per unit area ( $N_{A} \frac{1}{A} ρ t$ ).

In the graph above, we can see the importance of the overvoltage $U$ by how the intensity increase with increasing $U_{0}$

4.13.9. Quiz#

Why is the overvoltage increasing so much while the cross section remains rather constant above the threshold?

Chapter 4 Spectroscopy

Contents

4.12. Chapter 4 Spectroscopy #

4.13. Generation of Characteristic X-Rays#

4.13.1. Load relevant python packages#

4.13.1.1. Check Installed Packages#

4.13.2. First we import the essential libraries#

4.13.3. X-Ray Families#

4.13.4. X-ray Nomenclature#

4.13.5. X-ray Weight of Lines#

4.13.6. Characteristic X-ray Intensity#

4.13.7. X-ray Production in a Thick Solid Sample#

4.13.8. X-ray Production in a Thin Foil#

4.13.9. Quiz#

4.13.10. Navigation#

Chapter 4 Spectroscopy

Contents

4.12. Chapter 4 Spectroscopy#

4.13. Generation of Characteristic X-Rays#

4.13.1. Load relevant python packages#

4.13.1.1. Check Installed Packages#

4.13.2. First we import the essential libraries#

4.13.3. X-Ray Families#

4.13.4. X-ray Nomenclature#

4.13.5. X-ray Weight of Lines#

4.13.6. Characteristic X-ray Intensity#

4.13.7. X-ray Production in a Thick Solid Sample#

4.13.8. X-ray Production in a Thin Foil#

4.13.9. Quiz#

4.13.10. Navigation#

4.12. Chapter 4 Spectroscopy #